One of the great things about teaching fractions to my Mathemateers group is that they knew pretty much nothing about them. This meant that whatever they learned would show oodles of progress – always good for impressing line managers.
(Not that it matters in this circumstance. I am the booster (remedial) teacher for the Year 6 group, therefore reporting to the Year 6 teacher who in turn reports to the Key Stage 2 Phase Leader. However I line manage both these people, so it’s less of a line and more of a circle…)
The assessment system we use showed that all the children in the group struggled with fractions. For example, Sarah‘s profile in ‘number’ looked like this:
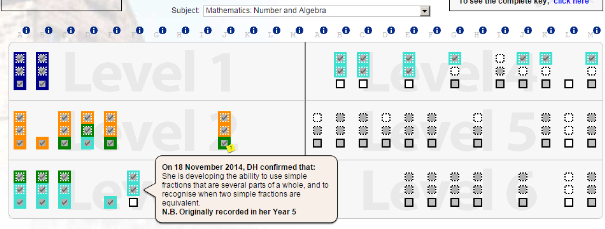
Of course when I asked Sarah some questions, it transpired that her prior assessment in fractions was, shall we say, over-ambitious, in that the assessment system said “she is developing the ability to use simple fractions that are several parts of a whole”, when actually she couldn’t do this question from ‘Recognizing Fractions 1‘ in the Khan Academy (which I have written about previously).

Of course there’s the whole issue about performance and learning here. Sometimes children really do know something, but for whatever reason they don’t show it. This is performance. Performance variation is one of the main reasons for the difficulty in carrying out accurate assessment in education.
But for me as a teacher, this is great. I can now teach some stuff to the children and show great progress. And that’s what I did. Pretty soon the children had motored on to ‘Recognizing Fractions 2’ and even managed to do questions like this by the end of the first week.

No I’m not saying this is world-record teaching, but it does show progress. And what’s great is there’s an image, you can talk about it with the child and then the child has to write down the answer in fraction notation. It’s the perfect move from the Pictorial to the abstract. The downside, if you only use the Khan Academy is that children don’t write down what they did in their books and so their progress isn’t there for external visitors. And that’s not good if you’re a very book-scrutiny focused kind of school.
What would be great would be if we had already moved on to the New National Curriculum. However, as you well know, Year 6 are still working to the old curriculum. You see Incerts have just released their tracking system for the new curriculum and it looks fantastic. Here’s a picture of the ticks I could make about Sarah’s fraction learning:
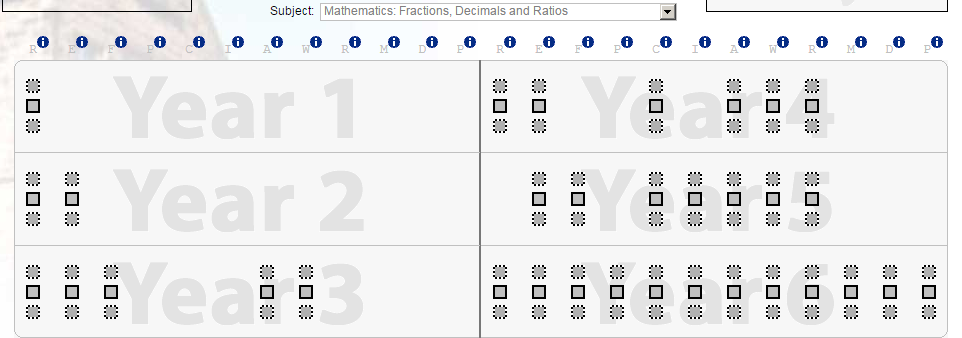
However I can’t use that for my current group because they’re in Year 6. Nope. I’m going to have to cope with the learning that’s actually happened in the children’s brains and their SATs results in a few weeks time. Speaking of that, the final tool I’ve used to show progress is the Testbase tool that is a store of all the previous SATs questions. Sounds boring, but it’s really, really handy at the stage of the school year when teaching in Year 6.



